CMF测量原理
以Micromotion的U型振动管为例，对Coriolis质量流量计的测量做定量分析：
Micromotion的U型振动管，通常振幅小于1mm，频率大约为80Hz.图3.3.3为振动中的测量管,流体被强制接受管子的垂直动量,在管子向上运动的振动半周期时,流入仪表的流体向下压,抵抗管子向上的力.反之,流出仪表流体存在向上的务,抗拒管子对其垂直量的减少而把管子向上推。两个反作用力合成引起流量测量管扭曲；这就是Coriolis效应。在振动的另外半周期，管子向下运动而扭曲方向就相反。图书馆显示一个流体，经过一个测量管，有一个质量m和速度V，它以相对O—O轴线的角速度ω旋转。因而产生Coriolis：


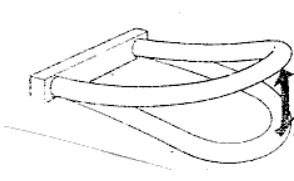
振动中的测量管




F=2mω V （1）
式中F和ω是矢量,Mj包含在长度L测量管中的质量(即半管中的流体质量)。



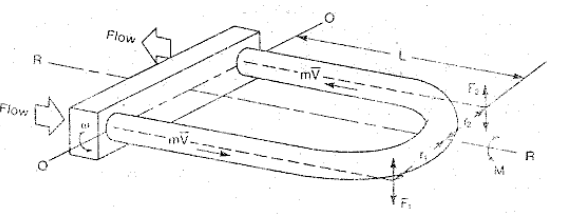
流体的入口和出口的速度矢量在方向上是相反的，如果从尾端观看这个测量管是两个引线（在图3.3.4中从R—R轴线看进去），由在入口与出口管线上的流体产生的力F1和F2在方向上是相反的，而大小相等。
由于管子相对O—O轴振动，这个力产生一个相对于R—R轴的振动力矩M（半径是r）。

M=F1·r1+F2·r2 （2）
由于F1=F2 r1=r2由式子（1）和（2）得出：
M=2Fr=4ω·V·m·r (3)

质量m是由密度ρ、管截面积A和长度L定义的，速度V是由单位时间的单位L定义的。质量流速Q是由每单位时间内通过的一个给出点质量决定的，那就是m=ρ·A·L及V=L/t 、Q=m/t这样通过取代Q=mv/L式中L是管长,
式(3)变成:M=4ω·r·Q·L (4)
力矩M产生一个角度偏转即扭转角θ,相对于R—R轴线。这扭转角在振动管移动的中点最大



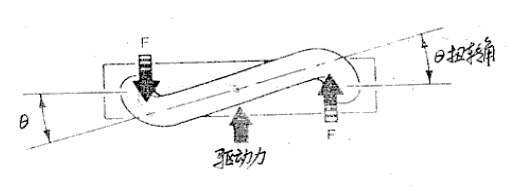
由测量管尾端所显示泊流体力

然而，由M产生的偏转被测量管的伸展弹力K所抵制，总之，对于任何的扭转弹力，扭矩T定义为T=Kθ（5）由于T=M，现在通过组合（4）与（5）式，质量流速Q能与偏转角度θ联系成相关式子。
Q= Kθ/4ω·r·L （6）
在管子轴线中心的移动速度Vt（线速度）乘以时间间隔，就与用几何图形表示的θ有关系。
Sinθ= Vt ·△t/r（7）
由于θ很小，它几乎等于Sinθ,对于小的旋转角Vt是ω和管长L的乘积，那就是θ=Sinθ、Vt=ωL，这样式（7）变成：
θ= ω·L·△t / r （8）
综合式（6）和（8）得出：
Q= （K·ω·L·△t K）/ （4r2ω·L 4r2） = △t （9）
这样质量流量计Q只与时间间隔t和几何常数成比例，Q与ω无关，所以说与测量管的振动频率无关。
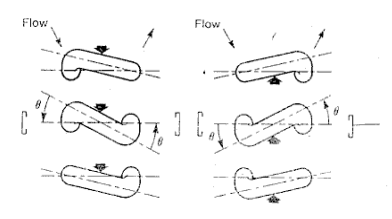
质量流量通过用电磁感应器测量偏转角θ获得，如图6所示，在横穿于测量管的中心轴线上的感应器，按一个时间函数测量θ，当没有流量时，在测量和轴线左右之间，上下撞击通过的时间差是0，而随着流量的增加引起θ增加，上下撞击信号之间的时间表差t也增加。测量扭曲多少与流量直接成正比，感应器将管子扭曲引起的时间差，传送到仪表的变送器进行处理转换。